Figure: A model including data of the four-fold structure of C60 molecules on the 2-fold surface of Al-Pd-Mn, with the cut away showing the relation to the five-fold facets.
The Fibonacci chain is a simple non-repeating mathematical sequence. It finds application surprisingly often in nature, for example in modelling population growth or in describing the patterns of facets found on the surface of a pineapple. It can be generated from some simple rules and is therefore well-ordered.
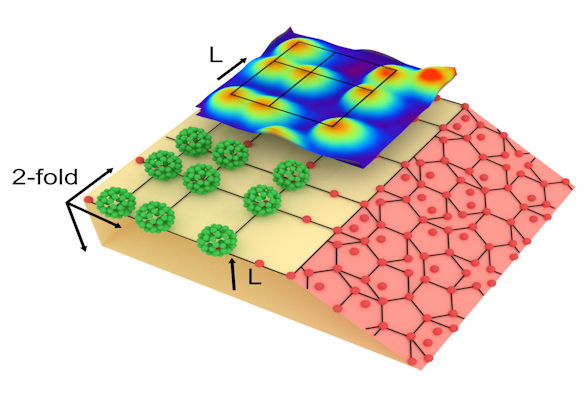
Consider two entities labelled L and S. Starting with L, apply rules such that L is replaced by LS and S is replaced by L. Then repeat the process. The terms of the sequence build as follows:
L (1)
LS (2)
LSL (3)
LSLLS (5)
LSLLSLSL (8)
LSLLSLSLLSLLS (13)
…..
Each term is the sum of the two preceding it.
The Fibonacci sequence can also be used to describe the structure of novel materials known as quasicrystals. Quasicrystals are generally metallic alloys whose structure differs from most crystals in that it is not based on a single simple repeating unit. This means that they generally have unusual symmetries – for example five-fold pentagonal or ten-fold decagonal rotational patterns.
They were discovered in 1982 by Professor Dan Shechtman who in 2011 received the Nobel Prize in Chemistry and was awarded an honorary degree by the University in 2014.
In 2002, Professor Ron Lifshitz pointed out that in theory it is possible to construct very simple quasicrystal models using the Fibonacci sequence which have common symmetries.
In his paper entitled “The square Fibonacci tiling” Professor Lifshitz developed a model of a quasicrystal with four-fold (square) symmetry, but also commented “to the best of my knowledge, no alloys or real quasicrystals exist with the structure of the square … Fibonacci tiling” (Lifshitz, Journal of Alloys and Compounds (2002) 342 186).
Now a team from the University’s Surface Science Research Centre and Department of Physics have discovered such a structure.
PhD student Sam Coates, Hem Raj Sharma, Professor Ronan McGrath and former PhD student Joe Smerdon (now at the University of Central Lancashire) found that when buckminsterfullerene (C60) molecules are deposited on the two-fold surface of the aluminium-palladium-manganese quasicrystal, they arrange into a square Fibonacci tiling – an exact physical realisation of Lifshitz’s model.
Their research paper `A molecular overlayer with the Fibonacci square grid structure’ (doi: 10.1038/s41467-018-05950-7) is published in Nature Communications.
Dr Sharma said: :“This structure is probably the simplest quasicrystal system yet found and potentially allows the creation of molecular thin films with intriguing structures and tuneable physical properties. These structures could include quasicrystalline molecular magnets and photonic materials. The work also demonstrates the use of molecules as a chemical sensors to identify different types of atoms on similar complicated metallic alloy surfaces.”
Professor Carsten Welsch, Head of the Physics Department, said: “This is an exciting result which extends the quasicrystal family beyond the forbidden symmetry systems previously observed. This research opens up exciting new opportunities, such as the design and fabrication of molecular arrays of a chosen magnetic behaviour. Congratulations to the whole team!”
You can read a blog article published on the Nature website by PHD student and first author Sam Coates about this research here.